FFT tide components.
Example showing how to extract the two principal tide components, M2 & S2, with Fourier analysis of a one month tide record.
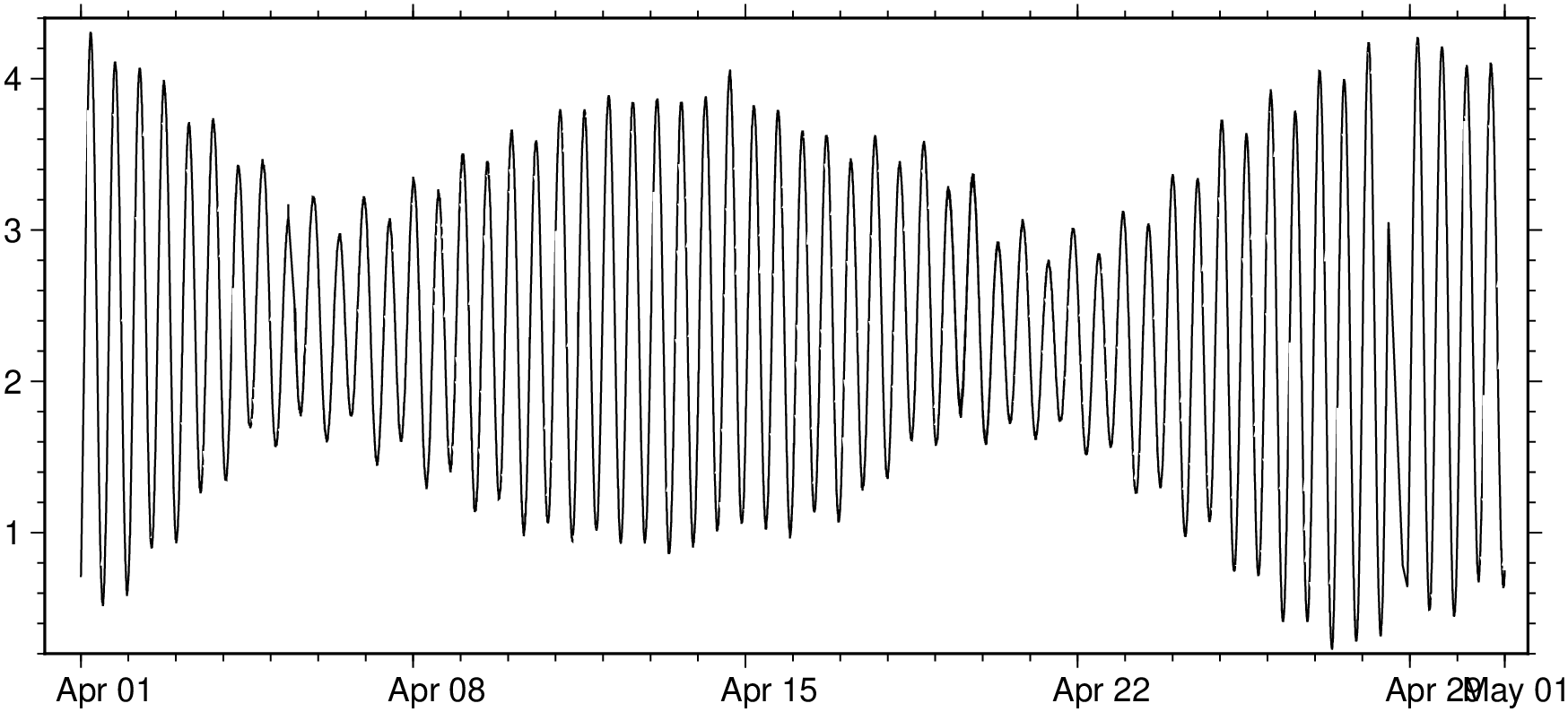
Get a one month maregram from a station in Galicia.
D = maregrams(code="fer1", days=30, starttime="2025-04-01T00:00:00");
viz(D, figsize=(14, 6))Resample the data to a constant time step of 60 seconds.
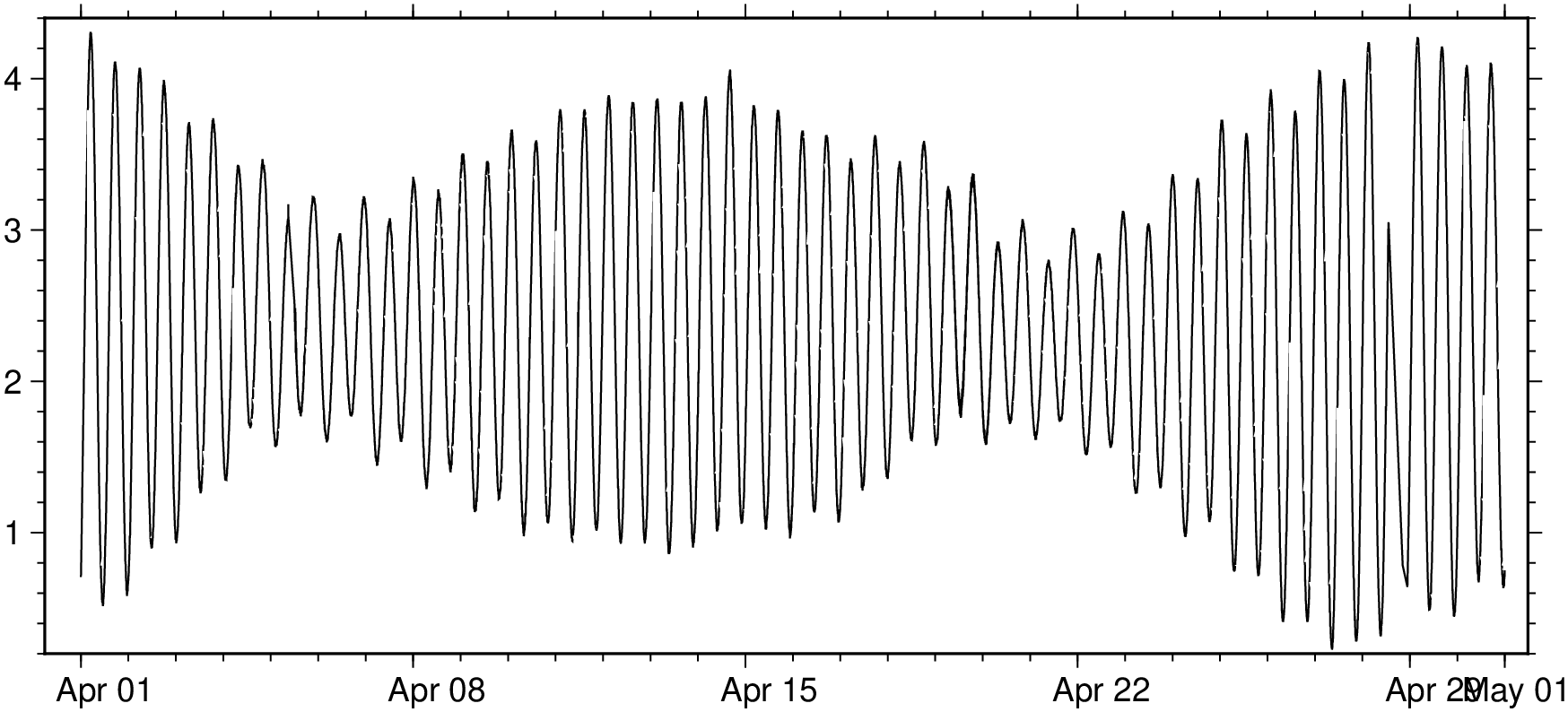
Ds = sample1d(D, T="2025-04-01T00:00:00/2025-05-01T00:00:00/60s");
viz(D, figsize=(14, 6))Set the parameters for this time series.
Fs = 1 / 60; # Sampling frequency (1 sample per 60 seconds)
L = size(Ds,1); # Length of signalFind the fundamental periods (tide components) in this tide record.
using GMT, FFTW
Y = fft(Ds[:,2] .- mean(Ds[:,2])); # FFTs require that we remove the mean (the zero frequency).
P = abs.(Y/L);
f = Fs * (0:(L/2)-1)/L;
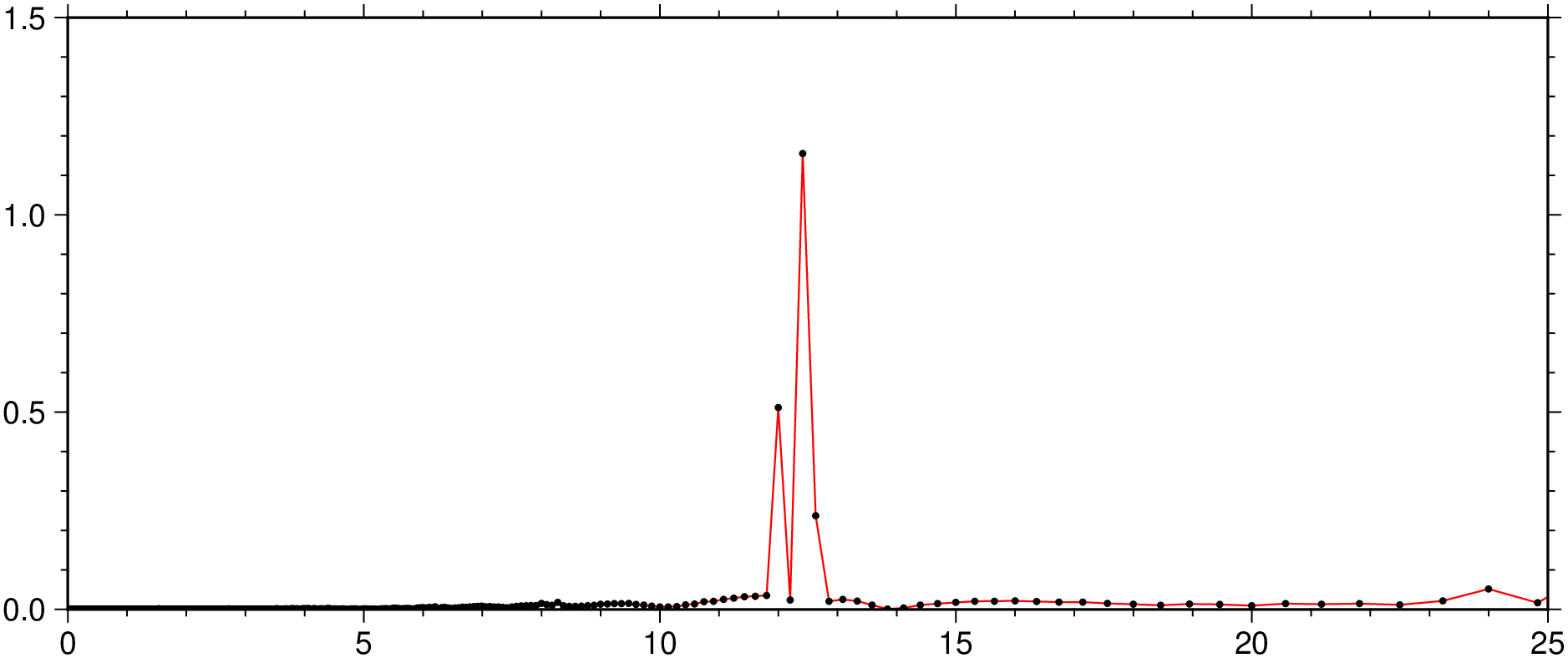
viz(1 ./ f ./ 3600, 2*P[1:length(f)], limits=(0,25,0,1.5), lc=:red, marker=:point, figsize=(15,6))The two frequencies can be found with:
findpeaks(P, min_height=0.2, xsorted=true)
4-element Vector{Int64}:
59
61
43142
43144Note that we got four but the last two are repeated as the FFT signal is symetric with respect to the N/2 position.
We can optain the periods in hours with
ff = fftfreq(L, 1/60);
T1 = 1/(ff[59])/3600
12.41408
T1 = 1/(ff[69])/3600
12.000278Which are the Principal Lunar (M2) and Principal Solar (S2) components.
© GMT.jl. Last modified: September 05, 2025. Website built with Franklin.jl and the Julia programming language.
These docs were autogenerated using GMT: v1.33.1